February 16, 2021 ⁓ 21 min read
I wanted to add moon phase information to my weather website. This is the PHP script I used to generate the HTML and how I styled it.

I have a Davis Instruments Vantage Pro2 Weather Station in my back yard. I use Wview running on a Raspberry Pi 2 to collect the data and generate the website. (I would include a link to Wview, but it seems the author has abandoned the project.) The default website theme that came with Wview was very 1990s in style. I wrote my own theme using modern semantic HTML and CSS. As part of the redesign, I wanted to display moon phase data to go along with the sun rise and set data — pretty standard almanac information.
The Wview HTML templates use include files, so all I needed to do was come up with a script that would periodically output HTML to an include file. Since Wview is written in PHP, I might as well go with that (it is guaranteed to be on any Wview server, after all). PHP has built-in functions for sun data (date_sun_info()), but minimal for moon data. I found MoonPhase PHP class by Samir Shah. It looked like it would return all of the data I wanted.
The Script
Using MoonPhase to get the data, I then worked out the HTML. Cutting to the chase, here is the script (available on in a GitHub repo):
#! /usr/bin/php
<?php
ini_set('display_errors', 1);
date_default_timezone_set('America/Los_Angeles');
ini_set('date.default_latitude', 33.9);
ini_set('date.default_longitude', -117.5);
$moon = new MoonPhase();
$phase_class = to_classname($moon->phase_name());
$illumination = round($moon->illumination() * 100);
$now = time();
$phases = array(
array('phase' => 'New Moon', 'time' => $moon->new_moon()),
array('phase' => 'First Quarter', 'time' => $moon->first_quarter()),
array('phase' => 'Full Moon', 'time' => $moon->full_moon()),
array('phase' => 'Last Quarter', 'time' => $moon->last_quarter()),
array('phase' => 'New Moon', 'time' => $moon->next_new_moon()),
array('phase' => 'First Quarter', 'time' => $moon->next_first_quarter()),
array('phase' => 'Full Moon', 'time' => $moon->next_full_moon()),
array('phase' => 'Last Quarter', 'time' => $moon->next_last_quarter())
);
echo <<<EOT
<p class="moon-phase">
<svg aria-hidden="true" focusable="false">
<use href="#icon-$phase_class" />
</svg>
{$moon->phase_name()}<br>
{$illumination}% illuminated
</p>
<div class="next-phases">
EOT;
for ($i = 0, $found = 0; $found < 4; $i++) {
if ($phases[$i]['time'] > $now) {
$found++;
$class = to_classname($phases[$i]['phase']);
$date = date( 'j M', $phases[$i]['time']);
echo <<<EOT
<div>
<svg aria-hidden="true" focusable="false">
<use href="#icon-{$class}" />
</svg><br>
$date<br>
{$phases[$i]['phase']}
</div>
EOT;
}
}
echo "</div>\n";
/**
* Convert string to class name.
*/
function to_classname($s) {
return preg_replace('/ /', '-', strtolower($s));
}
/**
* Moon phase calculation class
* Adapted for PHP from Moontool for Windows (http://www.fourmilab.ch/moontoolw/)
* by Samir Shah (http://rayofsolaris.net)
* License: MIT
**/
//namespace Solaris;
class MoonPhase {
private $timestamp;
private $phase;
private $illum;
private $age;
private $dist;
private $angdia;
private $sundist;
private $sunangdia;
private $synmonth;
private $quarters = null;
function __construct( $pdate = null ) {
if( is_null( $pdate ) )
$pdate = time();
/* Astronomical constants */
$epoch = 2444238.5; // 1980 January 0.0
/* Constants defining the Sun's apparent orbit */
$elonge = 278.833540; // Ecliptic longitude of the Sun at epoch 1980.0
$elongp = 282.596403; // Ecliptic longitude of the Sun at perigee
$eccent = 0.016718; // Eccentricity of Earth's orbit
$sunsmax = 1.495985e8; // Semi-major axis of Earth's orbit, km
$sunangsiz = 0.533128; // Sun's angular size, degrees, at semi-major axis distance
/* Elements of the Moon's orbit, epoch 1980.0 */
$mmlong = 64.975464; // Moon's mean longitude at the epoch
$mmlongp = 349.383063; // Mean longitude of the perigee at the epoch
$mlnode = 151.950429; // Mean longitude of the node at the epoch
$minc = 5.145396; // Inclination of the Moon's orbit
$mecc = 0.054900; // Eccentricity of the Moon's orbit
$mangsiz = 0.5181; // Moon's angular size at distance a from Earth
$msmax = 384401; // Semi-major axis of Moon's orbit in km
$mparallax = 0.9507; // Parallax at distance a from Earth
$synmonth = 29.53058868; // Synodic month (new Moon to new Moon)
$this->synmonth = $synmonth;
$lunatbase = 2423436.0; // Base date for E. W. Brown's numbered series of lunations (1923 January 16)
/* Properties of the Earth */
// $earthrad = 6378.16; // Radius of Earth in kilometres
// $PI = 3.14159265358979323846; // Assume not near black hole
$this->timestamp = $pdate;
// pdate is coming in as a UNIX timstamp, so convert it to Julian
$pdate = $pdate / 86400 + 2440587.5;
/* Calculation of the Sun's position */
$Day = $pdate - $epoch; // Date within epoch
$N = $this->fixangle((360 / 365.2422) * $Day); // Mean anomaly of the Sun
$M = $this->fixangle($N + $elonge - $elongp); // Convert from perigee co-ordinates to epoch 1980.0
$Ec = $this->kepler($M, $eccent); // Solve equation of Kepler
$Ec = sqrt((1 + $eccent) / (1 - $eccent)) * tan($Ec / 2);
$Ec = 2 * rad2deg(atan($Ec)); // True anomaly
$Lambdasun = $this->fixangle($Ec + $elongp); // Sun's geocentric ecliptic longitude
$F = ((1 + $eccent * cos(deg2rad($Ec))) / (1 - $eccent * $eccent)); // Orbital distance factor
$SunDist = $sunsmax / $F; // Distance to Sun in km
$SunAng = $F * $sunangsiz; // Sun's angular size in degrees
/* Calculation of the Moon's position */
$ml = $this->fixangle(13.1763966 * $Day + $mmlong); // Moon's mean longitude
$MM = $this->fixangle($ml - 0.1114041 * $Day - $mmlongp); // Moon's mean anomaly
$MN = $this->fixangle($mlnode - 0.0529539 * $Day); // Moon's ascending node mean longitude
$Ev = 1.2739 * sin(deg2rad(2 * ($ml - $Lambdasun) - $MM)); // Evection
$Ae = 0.1858 * sin(deg2rad($M)); // Annual equation
$A3 = 0.37 * sin(deg2rad($M)); // Correction term
$MmP = $MM + $Ev - $Ae - $A3; // Corrected anomaly
$mEc = 6.2886 * sin(deg2rad($MmP)); // Correction for the equation of the centre
$A4 = 0.214 * sin(deg2rad(2 * $MmP)); // Another correction term
$lP = $ml + $Ev + $mEc - $Ae + $A4; // Corrected longitude
$V = 0.6583 * sin(deg2rad(2 * ($lP - $Lambdasun))); // Variation
$lPP = $lP + $V; // True longitude
$NP = $MN - 0.16 * sin(deg2rad($M)); // Corrected longitude of the node
$y = sin(deg2rad($lPP - $NP)) * cos(deg2rad($minc)); // Y inclination coordinate
$x = cos(deg2rad($lPP - $NP)); // X inclination coordinate
$Lambdamoon = rad2deg(atan2($y, $x)) + $NP; // Ecliptic longitude
$BetaM = rad2deg(asin(sin(deg2rad($lPP - $NP)) * sin(deg2rad($minc)))); // Ecliptic latitude
/* Calculation of the phase of the Moon */
$MoonAge = $lPP - $Lambdasun; // Age of the Moon in degrees
$MoonPhase = (1 - cos(deg2rad($MoonAge))) / 2; // Phase of the Moon
// Distance of moon from the centre of the Earth
$MoonDist = ($msmax * (1 - $mecc * $mecc)) / (1 + $mecc * cos(deg2rad($MmP + $mEc)));
$MoonDFrac = $MoonDist / $msmax;
$MoonAng = $mangsiz / $MoonDFrac; // Moon's angular diameter
// $MoonPar = $mparallax / $MoonDFrac; // Moon's parallax
// store results
$this->phase = $this->fixangle($MoonAge) / 360; // Phase (0 to 1)
$this->illum = $MoonPhase; // Illuminated fraction (0 to 1)
$this->age = $synmonth * $this->phase; // Age of moon (days)
$this->dist = $MoonDist; // Distance (kilometres)
$this->angdia = $MoonAng; // Angular diameter (degrees)
$this->sundist = $SunDist; // Distance to Sun (kilometres)
$this->sunangdia = $SunAng; // Sun's angular diameter (degrees)
}
private function fixangle($a) {
return ( $a - 360 * floor($a / 360) );
}
// KEPLER -- Solve the equation of Kepler.
private function kepler($m, $ecc) {
$epsilon = 0.000001; // 1E-6
$e = $m = deg2rad($m);
do {
$delta = $e - $ecc * sin($e) - $m;
$e -= $delta / ( 1 - $ecc * cos($e) );
}
while ( abs($delta) > $epsilon );
return $e;
}
/* Calculates time of the mean new Moon for a given
base date. This argument K to this function is the
precomputed synodic month index, given by:
K = (year - 1900) * 12.3685
where year is expressed as a year and fractional year.
*/
private function meanphase($sdate, $k){
// Time in Julian centuries from 1900 January 0.5
$t = ( $sdate - 2415020.0 ) / 36525;
$t2 = $t * $t;
$t3 = $t2 * $t;
$nt1 = 2415020.75933 + $this->synmonth * $k
+ 0.0001178 * $t2
- 0.000000155 * $t3
+ 0.00033 * sin( deg2rad( 166.56 + 132.87 * $t - 0.009173 * $t2 ) );
return $nt1;
}
/* Given a K value used to determine the mean phase of
the new moon, and a phase selector (0.0, 0.25, 0.5,
0.75), obtain the true, corrected phase time.
*/
private function truephase($k, $phase){
$apcor = false;
$k += $phase; // Add phase to new moon time
$t = $k / 1236.85; // Time in Julian centuries from 1900 January 0.5
$t2 = $t * $t; // Square for frequent use
$t3 = $t2 * $t; // Cube for frequent use
$pt = 2415020.75933 // Mean time of phase
+ $this->synmonth * $k
+ 0.0001178 * $t2
- 0.000000155 * $t3
+ 0.00033 * sin( deg2rad( 166.56 + 132.87 * $t - 0.009173 * $t2 ) );
$m = 359.2242 + 29.10535608 * $k - 0.0000333 * $t2 - 0.00000347 * $t3; // Sun's mean anomaly
$mprime = 306.0253 + 385.81691806 * $k + 0.0107306 * $t2 + 0.00001236 * $t3; // Moon's mean anomaly
$f = 21.2964 + 390.67050646 * $k - 0.0016528 * $t2 - 0.00000239 * $t3; // Moon's argument of latitude
if ( $phase < 0.01 || abs( $phase - 0.5 ) < 0.01 ) {
// Corrections for New and Full Moon
$pt += (0.1734 - 0.000393 * $t) * sin( deg2rad( $m ) )
+ 0.0021 * sin( deg2rad( 2 * $m ) )
- 0.4068 * sin( deg2rad( $mprime ) )
+ 0.0161 * sin( deg2rad( 2 * $mprime) )
- 0.0004 * sin( deg2rad( 3 * $mprime ) )
+ 0.0104 * sin( deg2rad( 2 * $f ) )
- 0.0051 * sin( deg2rad( $m + $mprime ) )
- 0.0074 * sin( deg2rad( $m - $mprime ) )
+ 0.0004 * sin( deg2rad( 2 * $f + $m ) )
- 0.0004 * sin( deg2rad( 2 * $f - $m ) )
- 0.0006 * sin( deg2rad( 2 * $f + $mprime ) )
+ 0.0010 * sin( deg2rad( 2 * $f - $mprime ) )
+ 0.0005 * sin( deg2rad( $m + 2 * $mprime ) );
$apcor = true;
} else if ( abs( $phase - 0.25 ) < 0.01 || abs( $phase - 0.75 ) < 0.01 ) {
$pt += (0.1721 - 0.0004 * $t) * sin( deg2rad( $m ) )
+ 0.0021 * sin( deg2rad( 2 * $m ) )
- 0.6280 * sin( deg2rad( $mprime ) )
+ 0.0089 * sin( deg2rad( 2 * $mprime) )
- 0.0004 * sin( deg2rad( 3 * $mprime ) )
+ 0.0079 * sin( deg2rad( 2 * $f ) )
- 0.0119 * sin( deg2rad( $m + $mprime ) )
- 0.0047 * sin( deg2rad ( $m - $mprime ) )
+ 0.0003 * sin( deg2rad( 2 * $f + $m ) )
- 0.0004 * sin( deg2rad( 2 * $f - $m ) )
- 0.0006 * sin( deg2rad( 2 * $f + $mprime ) )
+ 0.0021 * sin( deg2rad( 2 * $f - $mprime ) )
+ 0.0003 * sin( deg2rad( $m + 2 * $mprime ) )
+ 0.0004 * sin( deg2rad( $m - 2 * $mprime ) )
- 0.0003 * sin( deg2rad( 2 * $m + $mprime ) );
if ( $phase < 0.5 ) // First quarter correction
$pt += 0.0028 - 0.0004 * cos( deg2rad( $m ) ) + 0.0003 * cos( deg2rad( $mprime ) );
else // Last quarter correction
$pt += -0.0028 + 0.0004 * cos( deg2rad( $m ) ) - 0.0003 * cos( deg2rad( $mprime ) );
$apcor = true;
}
if (!$apcor) // function was called with an invalid phase selector
return false;
return $pt;
}
/* Find time of phases of the moon which surround the current date.
Five phases are found, starting and
ending with the new moons which bound the current lunation.
*/
private function phasehunt() {
$sdate = $this->utctojulian( $this->timestamp );
$adate = $sdate - 45;
$ats = $this->timestamp - 86400 * 45;
$yy = (int) gmdate( 'Y', $ats );
$mm = (int) gmdate( 'n', $ats );
$k1 = floor( ( $yy + ( ( $mm - 1 ) * ( 1 / 12 ) ) - 1900 ) * 12.3685 );
$adate = $nt1 = $this->meanphase( $adate, $k1 );
while (true) {
$adate += $this->synmonth;
$k2 = $k1 + 1;
$nt2 = $this->meanphase( $adate, $k2 );
// if nt2 is close to sdate, then mean phase isn't good enough, we have to be more accurate
if( abs( $nt2 - $sdate ) < 0.75 )
$nt2 = $this->truephase( $k2, 0.0 );
if ( $nt1 <= $sdate && $nt2 > $sdate )
break;
$nt1 = $nt2;
$k1 = $k2;
}
// results in Julian dates
$data = array(
$this->truephase( $k1, 0.0 ),
$this->truephase( $k1, 0.25 ),
$this->truephase( $k1, 0.5 ),
$this->truephase( $k1, 0.75 ),
$this->truephase( $k2, 0.0 ),
$this->truephase( $k2, 0.25 ),
$this->truephase( $k2, 0.5 ),
$this->truephase( $k2, 0.75 )
);
$this->quarters = array();
foreach( $data as $v )
$this->quarters[] = ( $v - 2440587.5 ) * 86400; // convert to UNIX time
}
/* Convert UNIX timestamp to astronomical Julian time (i.e. Julian date plus day fraction). */
private function utctojulian( $ts ) {
return $ts / 86400 + 2440587.5;
}
private function get_phase( $n ) {
if( is_null( $this->quarters ) )
$this->phasehunt();
return $this->quarters[$n];
}
/* Public functions for accessing results */
function phase(){
return $this->phase;
}
function illumination(){
return $this->illum;
}
function age(){
return $this->age;
}
function distance(){
return $this->dist;
}
function diameter(){
return $this->angdia;
}
function sundistance(){
return $this->sundist;
}
function sundiameter(){
return $this->sunangdia;
}
function new_moon(){
return $this->get_phase( 0 );
}
function first_quarter(){
return $this->get_phase( 1 );
}
function full_moon(){
return $this->get_phase( 2 );
}
function last_quarter(){
return $this->get_phase( 3 );
}
function next_new_moon(){
return $this->get_phase( 4 );
}
function next_first_quarter(){
return $this->get_phase( 5 );
}
function next_full_moon(){
return $this->get_phase( 6 );
}
function next_last_quarter(){
return $this->get_phase( 7 );
}
function phase_name() {
$names = array( 'New Moon', 'Waxing Crescent', 'First Quarter', 'Waxing Gibbous', 'Full Moon', 'Waning Gibbous', 'Last Quarter', 'Waning Crescent', 'New Moon' );
// There are eight phases, evenly split. A "New Moon" occupies the 1/16th phases either side of phase = 0, and the rest follow from that.
return $names[ floor( ( $this->phase + 0.0625 ) * 8 ) ];
}
}
Set Up
The script needs your time zone and location. These are set at the top:
date_default_timezone_set('America/Los_Angeles');
ini_set('date.default_latitude', 33.9);
ini_set('date.default_longitude', -117.5);
I placed the script in /usr/local/bin and set this cron entry to call it:
# Calculate current moon phase
0 */2 * * * /usr/local/bin/moondata > /usr/local/etc/wview/html/moon.incx
Notes
The $phases array contains info on the quarter phases of this cycle and the next. The reason for that is that some of the phases of this cycle may now be in the past. We only want the next four phases. Here is the loop that goes through $phases and outputs the first four phases not in the past:
for ($i = 0, $found = 0; $found < 4; $i++) {
if ($phases[$i]['time'] > $now) {
$found++;
⋮
}
}
HTML
Here is sample output of the script:
<p class="moon-phase">
<svg aria-hidden="true" focusable="false">
<use href="#icon-waxing-cresent" />
</svg>
Waxing Cresent<br>
26% illuminated
</p>
<div class="next-phases">
<div>
<svg aria-hidden="true" focusable="false">
<use href="#icon-first-quarter" />
</svg><br>
19 Feb<br>
First Quarter
</div>
<div>
<svg aria-hidden="true" focusable="false">
<use href="#icon-full-moon" />
</svg><br>
27 Feb<br>
Full Moon
</div>
<div>
<svg aria-hidden="true" focusable="false">
<use href="#icon-last-quarter" />
</svg><br>
5 Mar<br>
Last Quarter
</div>
<div>
<svg aria-hidden="true" focusable="false">
<use href="#icon-new-moon" />
</svg><br>
13 Mar<br>
New Moon
</div>
</div>
The HTML is pretty straightforward. More on the SVG icons later.
Here is the section of index.incx that pulls in moon.incx.
<div class="moon">
<table class="mini-stats">
<thead>
<tr>
<th scope="row">Moon</th>
<th scope="col">Rise</th>
<th scope="col">Set</th>
</tr>
</thead>
<tbody>
<tr>
<td></td>
<td>
<!--moonriseTime-->
</td>
<td>
<!--moonsetTime-->
</td>
</tr>
</tbody>
</table>
<!--include moon.inc-->
</div>
CSS
There is not much to the styling. Flexbox makes the positioning easy. Oh, the hoops we had to jump through to try to do this before flexbox.
/* Moon phases */
.moon {
display: flex;
flex-direction: column;
align-items: flex-start;
}
.moon-phase {
display: flex;
align-items: center;
line-height: 1.2;
}
.moon-phase svg {
width: 2em;
height: 2em;
margin-right: 4px;
}
.next-phases {
display: flex;
align-items: center;
text-align: center;
border-top: 2px solid var(--gray3);
font-size: .75rem;
line-height: 1.25;
}
.next-phases svg {
width: 2em;
height: 2em;
}
.next-phases div+div {
margin-left: 8px;
}
Icons
Finding suitable moon phase icons was a bit of a chore. A lot of the icons sets were incomplete, not including all eight phases or were not to my liking. I ended up with a set from Wiki Commons. I did modify them to “correct” the stroke width and combined them into a single file as sprites. The SVG file gets included into the footer.
<svg style="display:none">
<defs>
<symbol id="icon-new-moon" viewBox="0 0 50 50">
<circle cx="25" cy="25" r="16" stroke-width="2"/>
</symbol>
<symbol id="icon-waxing-crescent" viewBox="0 0 50 50">
<circle stroke-width="2" fill="none" r="16" cy="25" cx="25"/>
<path stroke-width="0" d="m25,9a16,16 0 0 0 0,32l0,-1.5a18,18 0 0 0 0,-29l0,-1.5z"/>
</symbol>
<symbol id="icon-first-quarter" viewBox="0 0 50 50">
<circle stroke-width="2" fill="none" r="16" cy="25" cx="25"/>
<path stroke-width="0" d="m25,9a16,16 0 0 0 0,32l0,-32z"/>
</symbol>
<symbol id="icon-waxing-gibbous" viewBox="0 0 50 50">
<circle cx="25" cy="25" r="16" fill="none" stroke-width="2"/>
<path d="m25,9a16,16 0 0 0 0,32l0,-1.5a18,18 0 0 1 0,-29l0,-1.5z" stroke-width="0"/>
</symbol>
<symbol id="icon-full-moon" viewBox="0 0 50 50">
<circle cx="25" cy="25" r="16" fill="none" stroke-width="2"/>
</symbol>
<symbol id="icon-waning-gibbous" viewBox="0 0 50 50">
<circle cx="25" cy="25" r="16" fill="none" stroke-width="2"/>
<path d="m25,9a16,16 0 0 1 0,32l0,-1.5a18,18 0 0 0 0,-29l0,-1.5z" stroke-width="0"/>
</symbol>
<symbol id="icon-last-quarter" viewBox="0 0 50 50">
<circle cx="25" cy="25" r="16" fill="none" stroke-width="2"/>
<path d="m25,9a16,16 0 0 1 0,32l0,-32z" stroke-width="0"/>
</symbol>
<symbol id="icon-waning-crescent" viewBox="0 0 50 50">
<circle stroke-width="2" fill="none" r="16" cy="25" cx="25"/>
<path stroke-width="0" d="m25,9a16,16 0 0 1 0,32l0,-1.5a18,18 0 0 1 0,-29l0,-1.5z"/>
</symbol>
</defs>
</svg>
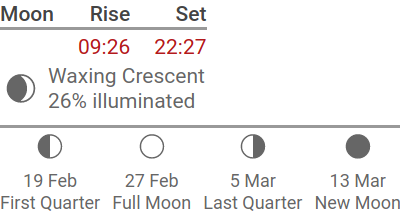
Final Result
After all of that code, the final result is almost anticlimatic. Sometimes you don’t realize just how much code is behind something that looks so simple.